Alcuin’s River Puzzles

The ecclesiastic, scholar, writer and poet, Alcuin of York (735-804), produced his puzzle book for the Emperor
Charlemagne, possibly the first ever-written. It was called Propositiones ad acuendos juvenes or ‘Puzzles
to Sharpen the Young’.
These three puzzles, propositions 17, 18 and 19 in the book, are all river crossing puzzles; the first is well-known,
the others less so.

XVIII. PROPOSITIO DE HOMINE ET CAPRA ET LVPO.
Homo quidam debebat ultra fluuium transferre lupum, capram, et fasciculum cauli. Et non potuit aliam nauem
inuenire, nisi quae duos tantum ex ipsis ferre ualebat. Praeceptum itaque ei fuerat, ut omnia haec ultra illaesa
omnino transferret. Dicat, qui potest, quomodo eis illaesis transire potuit?
This is roughly what the Latin says.
“A man had to carry a wolf, a goat, and a bunch of cabbage[s] across the river. And he could find no other ship,
except such as was capable of carrying only two of them. He had therefore been ordered to transfer all these
beyond unharmed. Let him who can, say how could he pass through them unscathed?”
To make it clear, he mustn’t leave the goat alone with the cabbages or the wolf alone with the goat, for
obvious reasons. How many times would he need to
cross the river from one side to the other in order to carry out his task?

Three men each with an unmarried sister wish to cross the river in the same two-seater boat. However Alcuin says each man “had lust for his neighbour’s sister”. More tactfully let’s say a sister would be in a compromising position if her brother was not with her at all times. Hint: Any man or woman can row the boat. Now how many times would the boat need to cross the river, either way, to ferry all the group across the river with decorum?

A man and a woman with their two children want to cross the river. The man and woman weigh the same and each child is half the weight of an adult. The boat can carry two people but can only hold the weight of one adult or it would sink. (Obviously a different boat to that used earlier.) Hint: Both the children can also row. How many times would the boat need to cross the river, either way, to carry the family across the river?
Alcuin’s answer: “I would first take the goat across and leave the wolf behind. Then I would return
and take the wolf across leaving it on the other side and bring the goat back. Leaving the goat behind, I would
take the cabbages over and leave them on the other side. I would return to pick up the goat I had taken across before.
There would be some healthy rowing without a storm of tearing.” Alcuin would have rowed a total of
7 times across the river.
Of course you could take the cabbages instead of the wolf across on the third trip and the wolf across on the
fifth trip but the number of trips is the same.
There is a shorter answer by Tom Crick:

If a woman in the boat AT the shore (but not ON the shore) counts as being by herself (that is, not in the presence
of any men on the shore), then the second puzzle can be solved in 9 one-way trips:
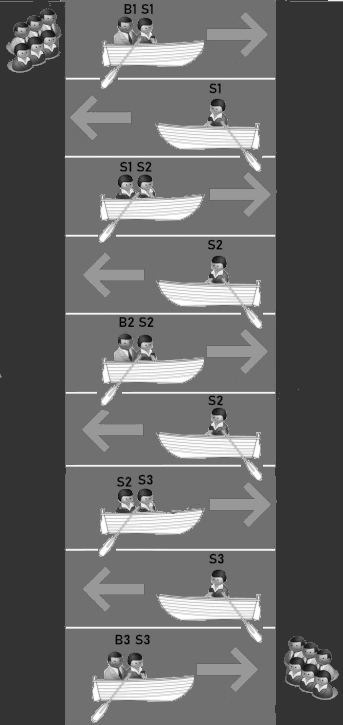
The third puzzle has the family crossing the river in 9 trips. The solution includes four
crossings with only one child in the boat and three crossings with two children in the boat.
